| Day | Outlook | Temperature | Humidity | Wind | PlayTennis |
| 1 | Sunny | Hot | High | Weak | No |
| 2 | Sunny | Hot | High | Strong | No |
| 3 | Overcast | Hot | High | Weak | Yes |
| 4 | Rain | Mild | High | Weak | Yes |
| 5 | Rain | Cool | Normal | Weak | Yes |
| 6 | Rain | Cool | Normal | Strong | No |
| 7 | Overcast | Cool | Normal | Strong | Yes |
| 8 | Sunny | Mild | High | Weak | No |
| 9 | Sunny | Cool | Normal | Weak | Yes |
| 10 | Rain | Mild | Normal | Weak | Yes |
| 11 | Sunny | Mild | Normal | Strong | Yes |
| 12 | Overcast | Mild | High | Strong | Yes |
| 13 | Overcast | Hot | Normal | Weak | Yes |
| 14 | Rain | Mild | High | Strong | No |
对于上面例子,如何判断是否要去playtennis?
可以采用决策树的方式。
决策树是一种以实例为基础的归纳学习算法。从无序列/无规则的数据中,推导出树形表示的分类判决。
优点:计算量小、显示清晰
缺点:容易过拟合(需要修枝)(譬如,使用day做判决,一一对应虽然很准确,但是不能用在其他地方)、对时间顺序的数据,需要过多预处理工作
ID3算法:
1、对于实例,计算各个属性的信息增益
2、对于信息增益最大的属性P作为根节点,P的各个取值的样本作为子集进行分类
3、对于子集下,若只含有正例或反例,直接得到判决;否则递归调用算法,再次寻找子节点

熵:表示随机变量的不确定性。
条件熵:在一个条件下,随机变量的不确定性。
信息增益:熵 - 条件熵,在一个条件下,信息不确定性减少的程度。
用信息增益最大的属性作为结点,是因为最终去不去打球的不确定性,在获得该属性的结果后,不确定性大大降低。
也就是说,该属性对于打球的选择很重要。
对于解决上述问题,
首先,计算系统熵,PlayTennis
P(No) = 5/14
P(Yes) = 9/14
Entropy(S) = -(9/14)*log(9/14)-(5/14)*log(5/14) = 0.94
然后,计算各个属性的熵。
譬如:Wind
其中,Wind中取值为weak的记录有8条,其中,playtennis的正例6个,负例2个;取值为strong的记录有6条,正例为3个,负例为3个。
Entrogy(weak) = -(6/8)*log(6/8)-(2/8)*log(2/8) = 0.811
Entrogy(strong) = -(3/6)*log(3/6)-(3/6)*log(3/6) = 1.0
对应的信息增益为:
Gain(Wind) = Entropy(S) – (8/14)* Entrogy(weak)-(6/14)* Entrogy(strong) = 0.048
同理,Gain(Humidity = 0.151;Gain(Outlook = 0.247;Gain(Temperature = 0.029
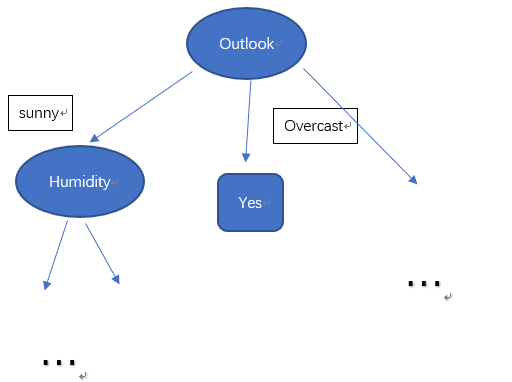
此时,可以得到跟节点为:Outlook
对应点决策树:
Outlook分为三个集合:
Sunny:{1,2,8,9,11},正例:2、反例:3
Overcast:{3,7,12,13},正例:4、反例:0
Rain:{4,5,6,10,14},正例:3、反例:2
至此,可以得到:
Sunny:
| Day | Outlook | Temperature | Humidity | Wind | PlayTennis |
| 1 | Sunny | Hot | High | Weak | No |
| 2 | Sunny | Hot | High | Strong | No |
| 8 | Sunny | Mild | High | Weak | No |
| 9 | Sunny | Cool | Normal | Weak | Yes |
| 11 | Sunny | Mild | Normal | Strong | Yes |
Entropy(S) = -(3/5)*log(3/5)-(2/5)*log(2/5) = 0.971
对于Wind,weak时,正例为1,反例为2;Strong时,正例为1,反例为1.
Entrogy(weak) = -(1/3)*log(1/3)-(2/3)*log(2/3) = 0.918
Entrogy(strong) = -(1/2)*log(1/2)-(1/2)*log(1/2) = 1
Gain(Wind) = Entropy(S) – 3/5* Entrogy(weak)-2/5* Entrogy(strong) = 0.0202
同理,Gain(Humidity) = 0.971;Gain(Temperature) = 0.571
此时,可以画出部分决策树:
其中,python代码:
import math#香农公式计算信息熵def calcShannonEnt(dataset): numEntries = len(dataset) labelCounts = {} for featVec in dataset: currentLabel = featVec[-1]#最后一位表示分类 if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0 labelCounts[currentLabel] +=1 shannonEnt = 0.0 for key in labelCounts: prob = float(labelCounts[key])/numEntries shannonEnt -= prob*math.log(prob, 2) return shannonEnt def CreateDataSet(): dataset = [['sunny', 'hot','high','weak', 'no' ], ['sunny', 'hot','high','strong', 'no' ], ['overcast', 'hot','high','weak', 'yes' ], ['rain', 'mild','high','weak', 'yes' ], ['rain', 'cool','normal','weak', 'yes' ], ['rain', 'cool','normal','strong', 'no' ], ['overcast', 'cool','normal','strong', 'yes' ], ['sunny', 'mild','high','weak', 'no' ], ['sunny', 'cool','normal','weak', 'yes' ], ['rain', 'mild','normal','weak', 'yes' ], ['sunny', 'mild','normal','strong', 'yes' ], ['overcast', 'mild','high','strong', 'yes' ], ['overcast', 'hot','normal','weak', 'yes' ], ['rain', 'mild','high','strong', 'no' ], ] labels = ['outlook', 'temperature', 'humidity', 'wind'] return dataset, labels#选取属性axis的值value的样本表def splitDataSet(dataSet, axis, value): retDataSet = [] for featVec in dataSet: if featVec[axis] == value: reducedFeatVec = featVec[:axis] reducedFeatVec.extend(featVec[axis+1:]) retDataSet.append(reducedFeatVec) return retDataSet#选取信息增益最大的属性作为节点def chooseBestFeatureToSplit(dataSet): numberFeatures = len(dataSet[0])-1 baseEntropy = calcShannonEnt(dataSet) bestInfoGain = 0.0 bestFeature = -1 for i in range(numberFeatures): featList = [example[i] for example in dataSet] uniqueVals = set(featList) newEntropy =0.0 for value in uniqueVals: subDataSet = splitDataSet(dataSet, i, value) prob = len(subDataSet)/float(len(dataSet)) newEntropy += prob * calcShannonEnt(subDataSet) infoGain = baseEntropy - newEntropy if(infoGain > bestInfoGain): bestInfoGain = infoGain bestFeature = i return bestFeature#对于属性已经用完,仍然没有分类的情况,采用投票表决的方法 def majorityCnt(classList): classCount ={} for vote in classList: if vote not in classCount.keys(): classCount[vote]=0 classCount[vote] += 1 return max(classCount) def createTree(dataSet, labels): classList = [example[-1] for example in dataSet] #类别相同停止划分 if classList.count(classList[0])==len(classList): return classList[0] #属性用完,投票表决 if len(dataSet[0])==1: return majorityCnt(classList) bestFeat = chooseBestFeatureToSplit(dataSet) bestFeatLabel = labels[bestFeat] myTree = {bestFeatLabel:{}} del(labels[bestFeat]) featValues = [example[bestFeat] for example in dataSet] uniqueVals = set(featValues) for value in uniqueVals: subLabels = labels[:] myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels) return myTree myDat,labels = CreateDataSet()tree = createTree(myDat,labels)print tree
在计算决策树的时候,sklearn库提供了决策树的计算方法(tree),但是,这个库提供的是:
scikit-learn uses an optimised version of the CART algorithm.
对于本文中使用的ID3算法是不支持的。
然而
该库支持ID3算法。
按照官网说明,注意安装时的依赖库的版本,该升级的升级,该安装的安装即可。‘
from id3 import Id3Estimatorfrom id3 import export_graphvizX = [['sunny', 'hot', 'high', 'weak'], ['sunny', 'hot', 'high', 'strong'], ['overcast', 'hot', 'high', 'weak'], ['rain', 'mild', 'high', 'weak'], ['rain', 'cool', 'normal', 'weak'], ['rain', 'cool', 'normal', 'strong'], ['overcast', 'cool', 'normal', 'strong'], ['sunny', 'mild', 'high', 'weak'], ['sunny', 'cool', 'normal', 'weak'], ['rain', 'mild', 'normal', 'weak'], ['sunny', 'mild', 'normal', 'strong'], ['overcast', 'mild', 'high', 'strong'], ['overcast', 'hot', 'normal', 'weak'], ['rain', 'mild', 'high', 'strong'], ]Y = ['no','no','yes','yes','yes','no','yes','no','yes','yes','yes','yes','yes','no']f = ['outlook','temperature','humidity','wind']estimator = Id3Estimator()estimator.fit(X, Y,check_input=True)export_graphviz(estimator.tree_, 'tree.dot', f)
然后通过GraphViz工具生成PDF
dot -Tpdf tree.dot -o tree.pdf
结果:

当然,你也可以进行预测判断:
print estimator.predict([['rain', 'mild', 'high', 'strong']])